まとめ
◇新型コロナウィルス(COVID-19)の封じ込めに失敗した現在、感染者数を制御しながら未感染者の免疫をどのように獲得して行くかが課題となる
◇免疫をつくるワクチンが開発されない限り、感染者数を抑える方法は、人と人との直接的な接触を抑える方法しかない
◇ワクチンができても、大量に供給されない限り、一気に新型コロナウィルスを抑え込むのは難しい
◇個人としては、ワクチンが十分供給されるまで出来るだけ新型コロナウィルスに罹らない生活を送るのが良いと考える
今回は中国南部の広東省で拡がった新型コロナウィルス(COVID-19)がテーマです。Alanna Shaikhさんによると、COVID-19も地球温暖化の影響だそうです。患者の数の情報は毎日公開されるが、全体として今後どうなるかのヒントになる情報が少ない。各国は新型コロナウィルスの封じ込めに失敗し、感染が世界規模で拡がって来た。家族や自分の健康管理、経済活動など、何をするにも予想が出来ないと動けない。誰かが新型コロナウィルスの感染を予想する数値モデルを公開しているのではないかと思い探すが見つけられなかった。そうなら自分で考えて予想しようとシミュレーションしてみました。
注意:念のため、私は医学の知識はありません。しかし、門外漢であることから思い切ったこともできると考えています。
ウイルスの感染モデル
感染症のもっとも基本的なモデルはSIRモデル 資料1)です。SIRはそれぞれ、S:感染症への免疫がない人数、I:感染者の人数、R:感染症から回復し免疫を獲得した人数を示す。時刻tのSをS(t)、IをI(t)およびRをR(t)とする。差分方程式で記述すると次の様に示される:
式(1) S(t+δt) – S(t) = -λx{S(t)/S(0)}xI(t)xδt
式(2) I(t+δt) – I(t) = λx{S(t)/S(0)}xI(t)xδt – γxI(t)xδt
式(3) R(t+δt) – R(t) = γxI(t)xδt
式(1)の免疫のない人の差分(時刻(t+δt)と時刻tでのSの変化)は免疫のない人の割合x感染者数に比例するとしている。λは比例定数である。λxδtで1人の感染者が免疫がない人に感染させる人数と考えてよい。式(2)は感染者の差分を示す。右辺は式(1)から新たに生まれる感染者数から回復者の数を減じている。γは比例定数で、γxδtは感染から回復する人の数と考えてよい。式(3)は免疫を獲得した人の差分を示す。
ワクチンの接種が可能となった場合を考慮して式(1)を次の様に変形した。免疫のない人の数はワクチン接種した人の数、つまり、βxδtだけ減ることになる。
式(4) S(t+δt) – S(t) = -λx{S(t)/S(0)}xI(t)xδt- βxδt
新型コロナウィルス(COVID-19)の感染力と致死率のデータは資料2)から得られる。基礎再生産数は1.6~4.2としている。これは、一人の感染者が何人に感染させるかを示す感染力の強さを表すパラメータです。致死率については、若年成人:0.1-0.2%、疾患をもつ高齢者:1%~となっています。
計算は資料1)と同様に表計算ソフトで行った。また、時間の単位はここでは「週」としています。新型コロナウィルス(COVID-19)はシンガポールなど熱帯地域にも拡散しているので夏になれば収束する期待も少なく、感染のスピードは季節で変化しないものとして扱いました。
ワクチンなしのケース
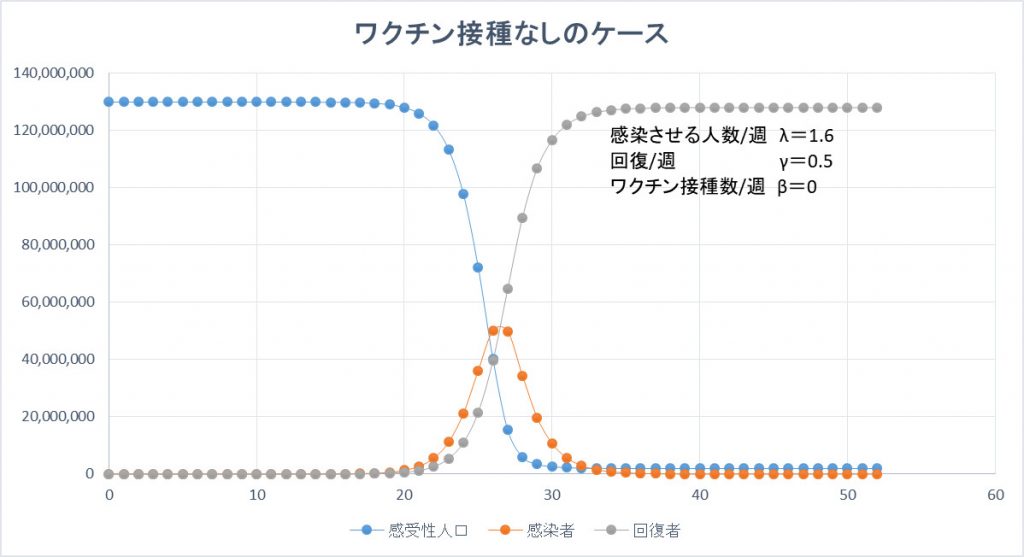
最初にワクチンなしの場合(2020年3月)を検討する。つまり、ウイルスに対する免疫の獲得手段はウイルスに感染し回復する方法しかない場合である。感染者1人が1週間の間でウイルスを感染させる人数を1.6人(=λxδt)とした。この数値は、感染者の隔離、人の集まりや移動を制限することで減らすことが可能である。感染者は2週間で回復し、免疫を獲得するものとした。
最初の1人の感染者から鼠算式に急増し、26週目で感染者はピークを迎え、50百万人となる。一方、56週目には全ての国民が免疫を獲得しこのウイルスの感染は止まる。ただし、この間、致死率を1%とすると、死亡者は1.3百万人が予測され人的被害は甚大なものとなる。
感染者1人が1週間の間でウイルスを感染させる人数(=λxδt)を大きくすると、感染者のピークはより高くなり、より早くやってくることになる。
ワクチンが潤沢な場合
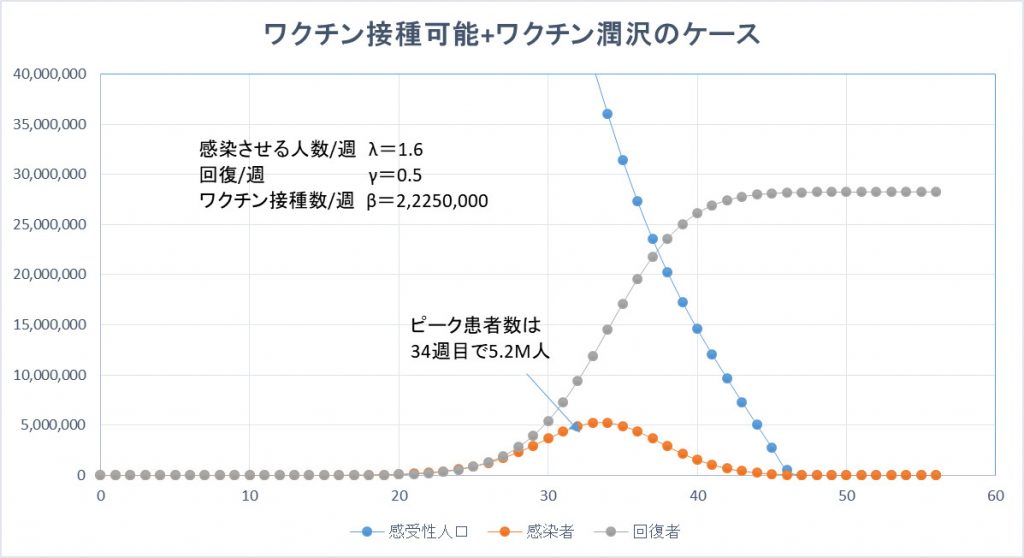
ワクチンが潤沢で入手可能な場合をシミュレーションする。ワクチンを接種した人は2週間後には必ず免疫ができると仮定した。
インフルエンザの例を参考とする。インフルエンザワクチンは通常、10月~11月の2ヵ月に渡って接種 資料3)し、12月~翌年3月の流行シーズンに備える。ワクチンの効果が出てくるのは2週間後とのこと。日本のインフルエンザ接種人数 資料4)は約17百万人とのことなので8週間で18百万人の速度で新型コロナウイルスのワクチンを接種したケースをシミュレーションした。あくまでワクチンが潤沢にあることが前提となっています。
このケースでは、新型コロナウイルスは63週目で完全に収束する。また、患者数のピークも5.2百万人とワクチンが利用できないケースの約1/10に抑えられる。新型コロナウイルスの延べ感染者数は28百万人となる。この結果、想定死者は28万人となり、ワクチンが利用できない場合の約1/5に減少する。ただし、治療薬が見つかりかつ秩序的な診療体制が維持できれば死者の数は激減すると推定される。
ワクチンが潤沢でない場合
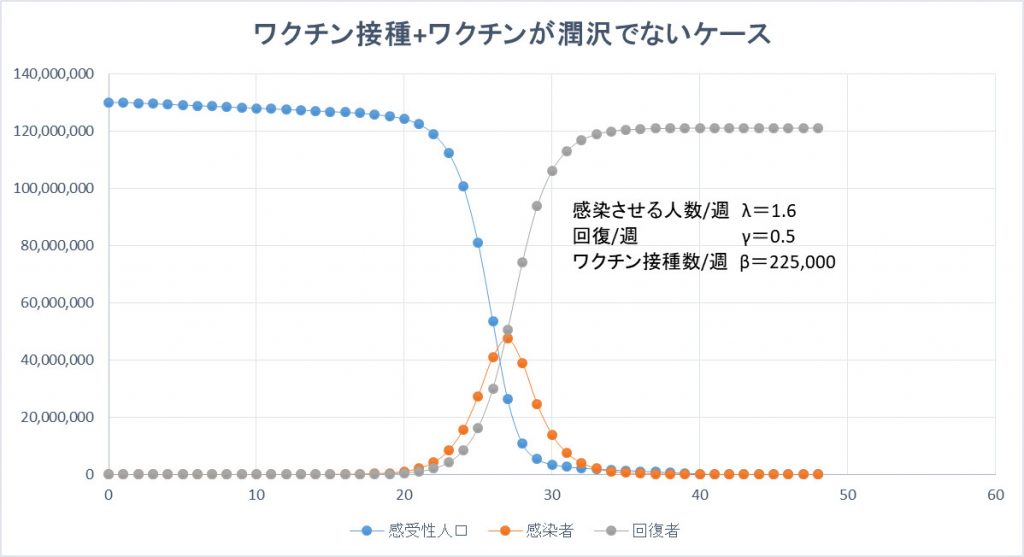
ワクチンが潤沢でない場合を想定したシミュレーションを行った。インフルエンザの例では接種時期10月~11月に備えてワクチンは準備されるので時間的な余裕があるが、新型コロナウイルスのような新たな感染症のワクチンは当面は取り合いになると予想される。したがって、ワクチンが潤沢でない場合を想定する必要がある。今回、通常のインフルエンザの1/10の速度での接種した場合でシミュレーションしてみた。
患者数のピークは47百万人で27週目に迎える。延べ感染者は121百万人となり、想定死者も121万人ののぼる。ワクチンが潤沢でない場合は、ワクチンが利用できない場合と大きな違いはない。
結論としては、大量のワクチンを確保し、一気に接種するのが好ましい。これが無理な場合は、人の接触や行動を制限してウイルスの感染速度を抑えながら、優先順位をつけてワクチンの接種を行い、徐々に制限を緩めて行くのが現実的と考える。その場合は長期になる覚悟が必要です。
参考文献
資料1)
https://www.rieti.go.jp/jp/columns/a01_0545.html
資料2)
https://costep.open-ed.hokudai.ac.jp/like_hokudai/contents/article/1866/
